题目分析

这个题目一眼看过去就是DP，但是状态转移方程比较难想。可以理解成爬楼梯的困难版本。

动态规划

我们记dp[i - 1]表示前i列的瓷砖能够铺满的最大方案数，dp[0]表示第一列能铺满的最大方案数，很简单，只能铺竖着放置的Domino，dp[0] = 1，dp[1]可以放置两个横的Domino，也可以放置两个竖的Domino。

dp[2]可以由dp[0]和dp[1]推导出来。但是图例中上面三种比较简单，dp[2] = dp[0] + dp[1]。dp[0] 表示可以由dp[0]放置两个横的Domino。dp[1]表示可以由dp[1]放置一个竖的Domino。

但是图例中下面两种状态如何维护呢？我们发现dp[2]还可以由一个上2下1的Trimino和一个上1下2的Trimino组成，也可以由一个上1下2的Trimino和一个上2下1的Trimino组成。

这时状态不够用了，需要增加维度，我们增加一维，为了叙述简单不妨用dyp[i]表示前i列的瓷砖，拼成差一个正方形的最大方案数。因为差上面一块和下面一块是对称的，不需要单独考虑。

则dp[2]除了dp[0] + dp[1]之外，还要考虑 + dyp[1]。且dyp[0] = 0，dyp[1] = 2。
而dyp[2] = 2 x dp[0] + dyp[1]，2 x dp[0]表示可以由dp[0]放置一个上2下1的Trimino或一个上1下2的Trimino，dyp[1]表示可以由dyp[1]放置一个横的Domino。

如下图所示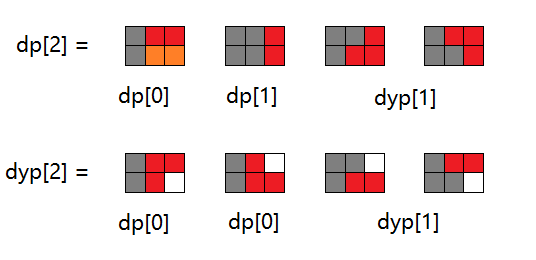

这种想法的难点是如何将上面比下面多1个和下面比上面多1个的情况都看作是dyp。

在代码中不用dyp，用一个二维数组表示，dp[i][0]表示上面的dp数组， dp[i][1]表示dyp数组。

算法的时间复杂度为O(n)，空间复杂度为O(n)。

class Solution {
    public static final int MOD = 1000000007;
    
    public int numTilings(int n) {
        if (n < 3) {
            return n;
        }
        int[][] dp = new int[n][2];
        dp[0][0] = 1;
        dp[0][1] = 0;
        dp[1][0] = 2;
        dp[1][1] = 2;
        for (int i = 2; i < n; i++) {
            dp[i][0] = ((dp[i - 1][0] + dp[i - 2][0]) % MOD + dp[i - 1][1]) % MOD;
            dp[i][1] = ((dp[i - 1][1] + dp[i - 2][0]) % MOD + dp[i - 2][0]) % MOD;
        }
        return dp[n - 1][0];
    }
}

动态规划优化

根据上面的分析可知

$$ \begin{cases} dp[i] = dp[i - 1] + dp[i - 2] + dyp[i - 1] \\ dyp[i] = dyp[i - 1] + 2 \times dp[i - 2] \end{cases} $$

因此可知
$$ dyp[i] = dyp[i - 1] + 2 \times dp[i - 2] = dyp[i - 2] + 2 \times dp[i - 3] + 2 \times dp[i - 2] = … = 2 \times (dp[0] + … + dp[i - 2]) $$

所以
$$ dp[i] = dp[i - 1] + dp[i - 2] + dyp[i - 1] = dp[i - 1] + dp[i - 2] + 2 \times (dp[0] + … + dp[i - 3]) $$

因为
$$ dp[i - 1] = dp[i - 2] + dp[i - 3] + dyp[i - 2] = dp[i - 2] + dp[i - 3] + 2 \times (dp[0] + … + dp[i - 4]) $$

可得
$$ dp[i] = dp[i - 1] + dp[i - 2] + 2 \times dp[i - 3] + 2 \times (dp[0] + … + dp[i - 3]) = 2 \times dp[i - 1] + dp[i - 3] $$

根据一步一步的递推，可得dp的递推关系式，下面就可以类似爬楼梯求解了。

dp只和前面的三个状态有关，因此可以使用滚动数组优化空间。

算法的时间复杂度为O(n)，空间复杂度为O(1)。

class Solution {
    public static final int MOD = 1000000007;
    
    public int numTilings(int n) {
        if (n < 3) {
            return n;
        }
        int a = 1;
        int b = 2;
        int c = 5;
        for (int i = 3; i < n; i++) {
            int cur = ((2 * c) % MOD + a) % MOD;
            a = b;
            b = c;
            c = cur;
        }
        return c;
    }
}

矩阵快速幂优化

矩阵快速幂不难，就是将$ f_n = 2 \times f_{n-1} + f_{n-3}$变成矩阵相乘的形式

$$ \begin{pmatrix} f_n \\ f_{n-1} \\ f_{n-2} \end{pmatrix} = \begin{pmatrix} 2 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} f_{n-1} \\ f_{n-2} \\ f_{n-3} \end{pmatrix} $$

$$ \begin{pmatrix} f_n \\ f_{n-1} \\ f_{n-2} \end{pmatrix} = \begin{pmatrix} 2 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}^{n - 3} \begin{pmatrix} f_3 \\ f_2 \\ f_1 \end{pmatrix} $$

然后利用快速幂的思想，在$O(log(n))$的时间内求解矩阵的幂即可。

算法的时间复杂度为O(log(n))，空间复杂度为O(1)。

class Solution {
    public static final int MOD = 1000000007;

    public int numTilings(int n) {
        if (n <= 2) {
            return n;
        }
        long[][] factor = new long[][]{{2, 0, 1}, {1, 0, 0}, {0, 1, 0}};
        long[][] base = new long[][]{{5}, {2}, {1}};
        int mi = n - 3;
        long[][] matrix = new long[][]{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
        while (mi != 0) {
            if ((mi & 1) != 0) {
                matrix = matrixMultiple(matrix, factor);
            }
            factor = matrixMultiple(factor, factor);
            mi >>= 1;
        }
        return (int) matrixMultiple(matrix, base)[0][0];
    }

    private long[][] matrixMultiple(long[][] a, long[][] b) {
        int r = a.length;
        int c = b[0].length;
        long[][] res = new long[r][c];
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                long cur = 0;
                for (int k = 0; k < a[0].length; k++) {
                    cur = (a[i][k] * b[k][j] + cur) % MOD;
                }
                res[i][j] = cur;
            }
        }
        return res;
    }
}

刷题总结

本题的思路很明确，就是DP。但是难度不小，难点在于如何表达状态的转移，并将一维转换成二维。